統計用語 雑記帳
日ごろ気になっていることを思いつくままに記します。個人的な見解です（間違いもありえます）。無断転載等、固くお断りします。
標本数
標本にふくまれる要素の数を「標本数」と称することがある。統計調査の専門家の会話や文書にもよく出てくる。誤解の恐れがほとんどないとはいえ、この呼称は少し気になる。
標本は、母集団の一部であるから集合として捉えられる。したがって、その中の要素の数は大きさであらわすのが普通である。英語では、sample size であるから、大きさで表現されている。日本語の教科書でも、多くは「標本の大きさ」という表現を頑なに守っている。だが、日常用語としては、「標本の大きさ」よりも「標本数」の方が多用されているように感じる。
このような表現が慣用化した一因は、日本語の「標本」が、ときとして、個々の要素を指す言葉としても使われることにあると思う。しかし、少なくとも有限母集団からの標本抽出の文脈では、「個々の要素は抽出単位と称し、標本はそれらの集まりを指す」という区別を守った方が誤解を生みにくい。余談だが、この雑文を書くために『広辞苑』第4版（岩波書店）で「標本」を引いたら、「①推測統計のため集団から抜き出した個々の要素」と記述されているのを発見した。
英語で書かれた教科書においては、sampleと言えば必ず抽出単位の集合を指す。このことは教科書だけに限らないようである。今朝読んだ、CBC（カナダにおけるNHKのような存在）のwebpage の世論調査の結果を報じた記事の最後に、つぎのような文があった。
It is considered to be
accurate, plus or minus, to within approximately 2.2 percentage points in 95
out of 100 samples.
最後の部分は、信頼係数を日常用語で表現しようとしたもので、「100組の（集合としての）標本を抽出すれば、（平均的に）95組の（集合としての）標本において」と解釈できる。
ついでながら、英語の教科書では（標本）抽出 sampling という用語も、集合としての標本を選ぶことに限定して使われている。標本抽出のために個々の抽出単位を選ぶことは抜き取り draw と表現される。日本語の教科書では両者の区別が曖昧であり、さらに抽出単位の意味で標本という用語がもちいられることがあるので、「標本を抽出する」という表現で個々の抽出単位の抜き取りをあらわすことが結構多い。
もっとも、多くの場合、標本抽出は1回、つまり、集合としての標本はひとつである。したがって、標本数100と聞いて（集合としての）標本が100組あると考える人はまずいない。冒頭で「誤解の恐れがほとんどない」と言ったのは、その意味である。しかし、日本語で書かれた統計関係の文書を英語に翻訳するとき、標本数を the number of samples と訳してしまう恐れは多分にあると思う。杞憂であればむしろ嬉しいのですが。
（2004年4月24日、5月20日加筆）
対数
変数変換の効果が抜群で解釈もしやすいため、対数変換は実証分析における常套手段のひとつである。ところが、私大文系型受験勉強のため数学から久しく（といっても、わずか数年のはずなのですが）離れていた新入生にとって、なじみの薄いものらしい。講義中に対数を使った同僚のH先生は、「先生、板書に出てくる十グラムというのはいったい何ですか」と学生に質問されて愕然となさったそうです。又聞きながら、作り話ではありません。log と10g、言われてみれば似てますが…。
私にはそれを笑う資格がない。かなり最近になって、知り合いのY先生から、「対数変換したデータから計算した標準偏差は、変動係数とほぼ等しい」ということを教わった。恥ずかしながら、そのときまでこのような重要な性質を知らずにいた。このことは、
であることからわかる。この他、対数変換には分布の歪みを矯正する効果も備わっている。変換したデータから計算した標準偏差が変動係数になるということだけなら、たとえば、おのおのの値を平均値で割れば事足りるけれども、分布の形状まで変わらない。
対数のような基本的な変数変換すらつかみきれていない。まだまだ修行が足りないようです。
（2004年4月24日、2004年5月21日加筆）
代表値
「分布の中心をあらわすという意味で分布を代表する値」と教わって、つい最近までそのように使っていた。これまで読んだ教科書にもそのように説明してあるものが多い。ところが、先日、分散や標準偏差などを「バラツキに関する代表値」と呼んでいる教科書に出くわした。手許の教科書をいくつか調べてみたところ、分布の中心の測度に限定せずに代表値をもちいているものが他にもあった。偶然かどうか、そのすべてが関西圏で教鞭をとられている方の著した教科書であった。関東や東北で教鞭を取られている方の教科書は、分布の中心の測度として代表値をもちいている。ついでながら、翻訳された教科書には、代表値という用語が使われていない。そういえば、代表値に対応する英語名を不明にして知らない。日本における統計用語として代表値がいつごろ登場し、どのように定着したのか、少し調べてみようと思う。
（2004年4月28日）
「トクサビ」
表題を見てピンと来た方は、この項読む必要ありません。官庁統計調査の略称についてです。官庁統計の名称には長いものが多いので、略称が愛用されるのは自然の成り行きです。調査名の痕跡が残っている点で、英語の acronym より優れているともいえます。問題は、省略の仕方に統一性がなく、結局丸暗記するしかないことにあります。文書では必ず正式名称が使用されるので、官庁統計コミュニティ？に接しないかぎり煩わされずにすむとはいえ、初めて聞くときには一瞬キョトンとします。このような経験をもつ人は、私だけではないはずです。以下、私の聞いたことのある略称を列挙します。正式名称は webpage などでお確かめください：(1)コクチョウ；(2)ロウチョウ；(3)シュウチョウ；(4)カケ（イ）チョウ；(5)ショウドウ；(6)ショウジツ；(7)コウジツ；(8)ショウコウジツ；(9)チンコウ；(10)セイドウ；(11)トクサビ；(12)キカツ；(13)ゼンブツ；(14)コウリ；(15)ロウトク；(16)ゼンショウ；(17)ベイビー；(18)マイキン；(19)エネバラ。
（2004年4月30日）
imputation
調査票の無回答部分や回答誤差がふくまれると判断される部分を、別の（適切だと思われる）値で置き換えることを指す。訳語は千差万別である。私の知る限りでも、代入や補完、補填、決め付け、補定、の5つがある（この他、経済統計で家賃などを擬制計算するときには帰属と訳される）。私自身は補完を使ってきた。しかし、補完（不足を補って完全にする）では、積極的な意味が強すぎるのではと最近反省している。理由はどうあれ、本当の観察値以外のものが代用されるのであるから、「完全になる」ことはありえない。中立的な用語としては代入、見た目の印象からは補定（一部の官庁で使われている造語？）あたりが候補といえようか。
（2004年4月30日）
後記：
Y先生から「補綴がもともとでは」との示唆をいただいた。おそらくこの説が正しいと思われる。補綴（ほてい・ほてつ）は、辞書にも載っていて、ほつれた箇所を繕うことである。意味もぴったりだ。「綴」（テイ、つづ・る）が常用漢字にないので、「定」に変更したのであろう。語義が変わってしまうようにも思えるけれど。
（2008年3月10日）
母集団
調査時点における調査対象全体の集合を指す。統計調査を実行するためには、母集団を操作的に定義し（すなわち、実査において母集団の構成員を判別できるような基準を定め）、フレーム（すなわち、操作的に定義された母集団の構成員を網羅するリスト）を用意しなければならない。しかし、母集団は刻一刻変化するので、完全なフレームは実際上存在しない。捕捉漏れや捕捉過剰が常に存在する。したがって、厳密には「母集団≠フレームに記載されている構成員」である。ところが、官庁統計に関する会議において、フレームのことを母集団と呼ぶことがある。細かいことではあるけれども、こうした混用は避けた方がよい。この種の会議では、捕捉漏れ・捕捉過剰が話題となることがしばしばあり、無用の混乱を招く恐れがある。母集団とフレーム（カタカナで具合が悪ければ母集団名簿）とを区別するだけで完封できる混乱である。
（2004年4月30日）
層別抽出における比推定
比推定とは、補助的な情報の力を借りて推定効率を向上させる手法のひとつである。たとえば、ある地域の販売額合計が推定対象である場合に、他の調査でその地域の従業者数合計がわかっていたとする。そのとき、販売額合計の推定量とおなじ公式で従業者数合計を推定し、もし、それが既知の従業者数合計の9/10であるとすれば、販売額も同じ比率で過小推定されている可能性が高いので、販売額合計の推定値を10/9倍する。販売額と従業者数との間に近似的な比例関係があれば、推定効率の向上が望める。
層別抽出において比推定を利用するとき、大きく分けて2通りの方法がある。ひとつは、おのおのの層において比推定を適用する方法であり、もうひとつは、おのおのの層においては比推定を適用せず、層ごとの推定値を合算する段階で比推定を適用する方法である。前者はseparate ratio estimatorと呼ばれ、個別比推定ないし分離比推定と訳される。後者はcombined (or compound) ratio estimatorと呼ばれ、総合比推定、結合比推定、複合比推定などと訳される。それぞれの訳語そのものは、内容から判断して妥当だと思う。
問題はそれらの組み合わせである。知り合いのY先生からうかがって何冊かの本を調べたところ、「分離&総合」や「分離&複合」、「個別&結合」などが見つかった。だが、不思議なことに、相性の良さそうな「個別&総合」や「分離&結合」は見当たらなかった。層別抽出のもとでの比推定を論じている日本語の文献がそれほど多くないこともあって、組み合わせの決定版はまだないようである。
Y先生に報告したところ、「では、今後『個別&総合』を流行らせよう」ということになった。はたして、成功するかどうか。
（2004年5月20日）
変形「3人の囚人の問題」
ベイズ統計学の教科書に頻出する話題のひとつに、「3人の囚人の問題」がある。いくつかのバリエーションがあるけれども、おおよそつぎのような問題である。「アランとバーナード、チャールズという3人の囚人がいる。3人のうち2人が処刑されることがわかっており、罪状から判断して刑を免れる確率は3人とも差がないとする。アランが看守に尋ねた。『私以外の2人のうち、少なくとも1人は確実に処刑される。したがって、自分以外に処刑される者1名の名前を教えてくれても、私の刑罰に関する情報にはならないはずだ。私以外で処刑される者の名前を1名教えてもらえませんか。』看守はアランの説得に応じて『バーナードは処刑される』と答えた。するとアランは心の中でほくそえんだ。『しめしめ。残るのはチャールズと俺だけだ。助かる可能性は五分五分だから、俺が処刑を免れる確率は1/3から1/2に上がった。』アランはほんとうに喜ぶべき状況にあるのか」。答えは、看守の発言を得たあとでも確率は1/3のまま。解答はベイズ統計学の教科書を参照されたい。なお、ここでの「確率」は主観確率と解釈するのが自然である。
この問題は授業でもときどき取り上げる。数年前、時間をかけて授業で説明したので、看守の発言から後ろのところを変更して試験問題を作った。「（看守が答えるところまでは上と同じ。）アランと看守の会話を盗み聞きしていたチャールズは心の中で思った。『よかった。残るのはアランと俺だけだ。可能性は五分五分だから、俺が処刑を免れる確率は1/3から1/2に上がった。』問題1：チャールズの言い分は正しいか。問題2：アランの助かる確率とチャールズのそれとを比較論評せよ」。
チャールズが助かる確率が2/3になることはすぐにわかる（これとても、正解者は多くなかった）。問題2でどのような解答が出てくるのかを楽しみにしていた。だが、設問の文言や時間制約のせいか、思ったよりも解答しにくかったようである。
アランもチャールズも立場は同じように思えるのに、助かる確率に違いが出てくるのはなぜか。この変形問題をゼミ合宿で取り上げたときには、つぎのようなヒントを出した。「チャールズになったつもりで、その場を頭の中で再現してごらん」。勘のいい学生は、このヒントで看守の発言が確率の評価にどのような影響をおよぼすかに気づく。実は、チャールズが聞いていること自体は問題の本質ではない。わざわざ話を変えたのは、実感を拠り所に問題解決の糸口を見つけやすいだろうと考えたからである。試験結果から判断する限り、空振りだったようだが…。
（2004年5月20日）
標準誤差率
官庁統計における標本推定値の精度をあらわすのに、標準誤差率という用語がある。たとえば、「目標精度として、標準誤差率を0.05とする」などと使われる。ところが、標準誤差率の定義には二通りの流儀があり、どちらが使われているかに注意しなければならない。いま、推定対象を
（母集団合計や母平均）とし、その標本推定量を 
、標本推定量の分散を 
とする。標準誤差率 
のひとつの定義は、標本推定量の変動係数、つまり 
であたえられる。目標精度が 
なら、
つまり 
となるように標本の大きさを定めれば目標精度が達成できる。
もうひとつの の定義は、推定量の相対的な乖離が確率0.95以上で を超えない、つまり 
であたえられる。目標精度を として正規近似を利用すれば、結局、
が成り立つように標本の大きさを定めれば、目標精度が達成できる。指定された標準誤差率の数値が同じでも、2番目の定義では、必要な標本の大きさが約2倍になる。
さて、層h における母数を 
とし、母集団における母数が 
とあらわせるとする。ただし、
だが、合計が1である必要はない。母集団合計や母平均はこのようにあらわせる。おのおのの層における母数の推定量
によって、母集団における母数の推定量を 
と定める。このとき、 の標準誤差率は、 の標準誤差率の最大値を上回らない。このことは以下のようにして示せる。標準誤差率の定義として1番目のタイプをもちいる（2番目のタイプでも結果は同様である）。
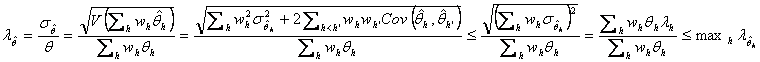
異なる層での標本抽出は相互に独立なのが普通であるけれども、上の式はそれを前提にしなくても成り立つ。この式から、たとえば、「おのおのの層の目標精度が0.05であれば、母集団推定量の標準誤差率は0.05を超えない」ことがわかる。最後の関係式は、少なくとも私には自明ではなかったので、備忘録として記します。
（2004年5月27日）
有意
統計学では「有意」がふたつの意味で使われる。ひとつは、「有意標本」の有意であり、意図・作為がある（無作為ではない）ということを指す。もうひとつは、仮説検定における「有意性」の有意であり、意味がある（重要である）ということを指す。英語では、前者が purposive であり、後者が significant である。訳語として間違いないとはいえ、異なる意味をひとつの言葉で表現していることは初学者にとって混乱のもとではないかと心配になる。実際上、それほど問題になっていないのは、「有意標本」が教科書でせいぜい1回しかあらわれないのに対し、「有意性」は頻繁にあらわれることによるのだろう。訳語として両方とも定着してしまっているから、いまさら「ゆうい」という音を変えるのは難しい。以前、「有為標本」と表記している本を見たことがある。しかし、有為の本来の意味は「才能があること」なので適切とはいえない（確信犯？）。何かいい知恵はないものだろうか。
（2004年6月24日）
乗法定理
初めて乗法定理を習ったとき、「条件つき確率の定義式を変形しただけの式がなぜ定理なのかしら」と不思議に感じた。その感覚はその後もずっと引きずったままであった。恥ずかしい話だが、ごく最近になってやっと「初等統計学のレベルにおいても、その有効性ゆえに乗法定理は定理に値する」と実感できるようになった。
いささか迂遠な説明をすればつぎのようになる。「複雑な問題を簡単な問題に分割し、分割した問題の解決を探ることによって、もとの複雑な問題が解決できる」とよく言われる。その一方で、われわれは「個別の解決が全体の解決につながるとはかぎらない」（合成の誤謬）ということを経済学で教わる。これらふたつの言説は両立しうるのか。
複雑な問題をうまく簡単な問題に分割（標本空間を制限）すれば解決（確率の評価）が簡単になる、というのは多くの場合正しい。だが、簡単な問題の解決（条件つき確率の評価）をもとの複雑な問題の解決（同時確率の評価）に複合し直すための手続き（乗法定理）が示されない限り、前者は後者の役に立たない。乗法定理が素晴らしいのは、その具体的な手続きをあたえていることにあると思う。先のふたつの言説のうち、最初のものは乗法定理に対応する手続きが簡単にえられる状況を暗黙裡に想定しており、ふたつ目のものはそのような手続きが必ずしも容易にはえられないことを指摘していると解釈できる。
乗法定理を有効に活用するためには、標本空間をうまく（つまり、条件つき確率の評価がしやすく、かつ、条件としてつかった事象の確率も評価しやすいように）制限することが肝要である。どうすれば「うまく」制限できるのかは問題によって異なり、乗法定理の内部から生み出されるものではない。有名な誕生日問題をあらためて眺めると、標本空間を巧みに制限することによって、極めて複雑な問題を初等統計学レベルで見事に解いていることがわかる。乗法定理の助けなしに解こうとすると、気が遠くなるほど面倒な計算をしなければならない。
（2005年3月22日）
具体例
統計用語ではありませんが、「わかりやすい具体例も、度が過ぎるのは考え物だ」という話をふたつ。まずは、その道の専門家に質問するときのこと。今も懇意にしていただいているS先生に初めて会ったとき、SASのプログラムについて質問した。具体例はできる限り簡単な方がわかりやすいとの信念をもっていた私は、100以上あるカテゴリーの数を2つに単純化して（そうすることで本質が見やすくなると思ったため）、このような状況でこういうことがやりたいのですけれど、とうかがった。数日の後、S先生からサンプル・プログラムをいただいた。私にわかりやすいように工夫なさったそのプログラムは、しかし、多数のカテゴリーを処理するには不向きであった（当然といえば当然）。そのことをメールでお伝えしたところ返信はなかった。後日、直接お会いしたときにお詫びがてら挨拶したところ、開口一番、「あなたは問題のスペックを落として説明しただろう。最初からあのような問題だとわかっていたら、私はもっと別の方法を考えた」という、いかにも工学博士らしいお叱りを受けた。この場合、カテゴリーの数が多いということも問題の本質の一部であり、勝手に省略してはいけなかったのである。お叱りを受けながら、「そうか。専門家にものを聞くときは、複雑なまま渡した方がかえって親切なんだ」と悟った次第であった。
もうひとつは学生からの質問に答えるときのこと。新学期が始まって間もないころ、ひとりの新入生が統計学の勉強の仕方について質問に来た。授業が目指しているものが見えず、初めて勉強する科目でもあるので、学習に不安を感じているとのことであった。あまりにも自信なさそうに見えたので、思い切って単純な例で代表値の意味やバラツキの大切さを力説した。説明が終わったとたん、件の学生いわく：「それって、小学生でもわかることじゃないですか。統計学って、そういうものなんですか？」
なにごとも行き過ぎは禁物のようです。
（2005年4月3日）
母集団数
最近になって、「母集団数」という表現を一度ならず目にした。いわんとするところ（母集団にふくまれている要素の数）はわかるものの、母集団も集合なので「母集団の大きさ」が正確な表現である。上の「標本数」の項で、この用語がなぜ定着してしまったのかについて私見を述べた。ところが、その理屈を「母集団数」には適用できそうにない。母集団（集団という字が使われている！）という用語をその構成要素と混用する習慣は政府統計の世界にもないからである。だが、さすがに｢母集団数｣にはかなり強い違和感を覚える。英語で the number of populations と書けば、誰でも「おかしい」と思うはずだ。気にしなければすむ話といえるのかどうか…。
（2007年4月3日）
動態統計
公的統計では、動態統計という用語が複数の意味で使われている。そして、公的統計に長年従事している人たちは無意識にそれらを使い分けている。こうした状況は、公的統計になじみのない者に戸惑いをあたえる。私自身、「構造統計と動態統計」という対比に初めて接したとき、なぜ両者が対概念となるのか不思議だった。以下で、公的統計における動態という用語の使い方を我流で整理する。
まず、人口統計における動態統計はフローを対象とした統計であることを意味する。たとえば、一年間に発生した出生・死亡などが人口動態統計の主要な対象である。これに対比されるのは、ストックを対象とする人口静態統計である。ある一時点における人口などが対象となる。人口統計では、これ以外の意味で動態という用語は使われない。
統計とは関係の薄い脱線になるけれども、経済学における静態（静学）・動態（動学）は人口統計とは別の意味で使われる。経済学では、静態は時間の変化を意識しない分析的な枠組み、動態は時間の変化を明示的に意識したそれである。人口統計における静態と動態の意味の区別に、経済学ではストックとフローが使われる。経済学を先に勉強した私は、人口統計における静態・動態の区別を後で習ったとき、ずいぶん紛らわしいと感じた。
動態統計に話をもどすと、第2に、調査項目を簡易にして頻繁（月次）に実施する調査を意味することがある。経済産業省の調査では動態をこの意味で用いている。生産動態統計調査や商業動態統計調査などが例である。この意味の動態統計に対比されるのが、調査項目を詳細にして長い周期で実施する構造統計である。先に挙げた統計に対しては、工業統計調査や商業統計調査がこれに当たる。ただし、動態統計をこのような意味で使うのは経済産業省に限られるようである。他の府省では、動態調査・構造調査という対比に代えて経常調査・周期調査（調査周期による調査の種類の区別）あるいは動向調査・構造調査（調査の名称の一部）という対比をもちいている。
ちなみに、人口動態統計（厚生労働省）と生産動態統計調査、商業動態統計調査の英語名称は、それぞれ、Vital Statistics of Japan と Current Survey of Production、Monthly Report on the Current Survey of Commerceとなっている。
（2011年4月17日）
バスケット項目
統計の整理に分類は必要である。分類の仕方が異なると複数の統計が比較しにくくなる。そのため、統計作成のためにとくに重要な分類については統一的な基準を定めて、統計作成者がこれを順守するようになっている。公的統計における分類基準の代表例として、日本標準産業分類と日本標準商品分類、日本標準職業分類があげられる。
どのように分類を作成しても、「どの分類にも入りにくい」という対象が必ず出現する。大分類・中分類・小分類・細分類と分類の基準が細かくなるほど、そうした対象が増える。時代の変化とともに、分類を作成したときには存在しなかったような新しい産業・製品・職業もあらわれる。しかし、分類である以上、どの対象もどこかの分類に属さなければならない。分類不能は許されない。
そこで、分類不能をなくす工夫として、「その他」という項目を用意する。「その他」と明示されることもあるし、「他に分類されないXX」と表現されることもある。こうした「その他」項目をバスケット項目とよぶ。命名の理由は寡聞にして知らないけれども、何でも入れておける項目、といった意味と勝手に解釈している。
うまく分類できない対象が入るのであるから、バスケット項目が肥大することは、作成した分類が現実に適応していないことを意味する。バスケット項目の構成比の上昇も、分類改訂の目安となる。
（2011年4月22日）
格付
公的統計の世界では、格付は、標準産業分類などにもとづいて調査客体を分類する作業またはその結果を意味する。一般の用語（債権の格付など）とは意味が異なる。
分類基準の作成と同様に、格付（分類基準の適用）も難しい。同じ条件のふたつの対象は必ず同じ格付にならなければならない。厳格に分類基準を適用するためには専門的な知識を要する。
格付は、統計の利用にも影響をおよぼす。たとえば、ある事業所が、産業分類をまたがる複数の事業で活動しているとき、通常は主業（もっとも大きな付加価値を創出している事業）によって産業が格付けられる。集計の際に、他の事業による付加価値も格付けされた産業でまとめられると、付加価値の総額は変わらないけれども、産業分類別の付加価値の合計は生産活動の実情と異なる。
格付が調査客体の回答に委ねられることもある。世帯統計において世帯員の勤め先の業種や本人の職業などを調査する場合などが典型的な例である。回答者の抱く産業・職業のイメージと、統計上の定義とが異ならないような工夫が調査票や回答手引きに求められる。
かなり前の日経新聞の「私の履歴書」欄で、横尾忠則氏が（私の記憶が正しければ）つぎのような趣旨のことを書いておられた：「デザイナーは職業だから本人が思ってもすぐにはなれないけれど、画家は生き方のことなので、思い立ったときになれる」。複数の職種に従事している場合、収入がもっとも多い職種を回答するのが国勢調査等での原則である。が、回答手引きに説明があっても、芸術に生きることを信条とする人が調査票にどう記入するであろうか。横尾氏の「私の履歴書」を読みながら、考え込んでしまった。
（2011年4月22日）
標本平均の標本分布
朝刊第一面の広告欄に『詳説 不正調査の法律問題』とあるのを見て、ちょっと驚いた。調査を装った訪問販売等が横行して、単行本が出版されるほどなのか、と早とちりしたからである。ところが、広告文を読むと、不正調査とは「不正の」調査のことだった。「不正な」調査ではなかった。
複数の単語をまとめて一語に合成できるのは便利である。他の言語にも散見される。しかし、平仮名で単語の役割を区別することが多い日本語では、合成の際に平仮名が欠落して意味が不明瞭になることがままある。不正調査はその一例である。
統計学の用語でもこの弊害が生じる。とくに翻訳で起こりやすい。その最たる例は、標本平均と標本分布である。両者で標本の意味が異なる。前者は「標本における」平均、後者は「標本抽出によって発生する」（統計量の）確率分布、である。英語では、sample mean と sampling distribution であるから、対象と行為との区別が一目瞭然である。憶測ながら、わが国では、標本分布を「標本における」分布と勘違いしている学生が少なくない。教える側に責任があるけれども、用語にも問題がある。とはいえ、（標本）抽出分布では、かえって意味不明になってしまいそうだ。日本の学校で標本平均の標本分布について誤解なく説明するのは、用語の面からも難しい。
（2011年4月23日）
断層
経済情勢の急変や調査方法の変更などによって、統計の集計結果の趨勢に大きな変化が発生すると、断層生じたという。経済情勢の変化は統計に反映されてしかるべきである。しかし、調査方法の変更による断層はこれと性質が異なる。
集計結果に差が生じるだけでは断層とはよべない。異時点では母集団における集計値が変化している。標本調査ではさらに標本誤差が発生する。標本の入れ替えによって集計値に大きな変化が発生したとしても、それを断層と即断するのは危険である。
私見では、何らかの理由によって、調査から発生する偏りに変化が生じることを断層と定義するのが適切である。この定義によると、調査方法を変更しても、断層が発生するとは限らない。たとえば、変更前も後も不偏な標本抽出にもとづいて調査が設計されていれば、標本誤差にふくまれる偏りはどちらも0となり、標本誤差内で断層はない。
では、なぜ調査方法の変更によって断層が発生しやすくなるのか。その理由は、変更によって非標本誤差の発生の仕方が変化するためである。非標本誤差は集計値の偏りに直結する。たとえば、調査員調査を郵送調査に変更すると、回答率に変化が生じた場合、回答者と無回答者とが調査項目から見て異質であれば偏りの入り方に差が生じる。そのときの差は断層とよぶに相応しい。
調査方法の変更による断層をこのように定義すると、ふたつのことが分かる。まず、断層の発生を識別することが難しい。一般に、非標本誤差を定量的に評価するのは困難である。したがって、調査方法変更後の調査をひとつだけ取り出して断層の有無を検証することは不可能に近い。変更後の調査結果をしばらく観察して、趨勢の水準と方向とに大きな変化が生じたかどうかを確認するのが現実的な検証方法である。ただし、時間の経過によって調査方法以外の要因も変化するので、傍証にしかすぎない。
ふたつ目に、たとえ断層の発生が確認できても、それが集計値の信頼性の低下を意味するとはかぎらないことである。どのような調査にも非標本誤差はふくまれる。母集団名簿の大幅な更新されて捕捉率が改善されるときのように、非標本誤差の縮小が予想されるのであれば、断層の発生は集計値の質の向上を意味する。調査方法の変更によって回答率が低下したとすると、断層の発生は集計値の質の低下を意味する。実際には、調査方法の変更が非標本誤差におよぼす影響の方向が判然としないことが多いので、断層のよしあしについて断定できない。
（2011年4月24日）
抽出デザインと抽出スキーム
抽出デザイン sampling design とは、出現可能な（集合としての）標本のひとつひとつに出現確率を割り当てた結果をあらわす。たとえば、大きさ10の母集団から大きさ3の標本を抽出するとき、出現可能な120組の標本のひとつひとつに出現確率を割り当てた結果である。
一方、抽出スキーム sampling scheme とは、デザインを実現する方法をあらわす。同じ抽出デザインを実現するのにも複数の抽出スキームがありうる。たとえば、先の120組の標本のどれもが等確率で出現する抽出デザイン（単純無作為抽出）考えると、(1)10本中3本の当たりくじのあるくじを引く、(2)120組の標本すべてに通し番号をつけておいて、1から120までの番号札（120枚）から1枚を無作為に抜き取る、のいずれの方法も抽出スキームたりうる。
推定量の統計理論的な性質を決めるのは抽出デザインである。抽出デザインが同じであれば、その実現の方法はどれであっても統計理論的な結論は同じになる。
しかし、標本抽出法の名称は抽出スキームにちなむことが多い。たとえば、二段抽出法という名称は、一段目に集落を抽出し、二段目に集落から最終抽出単位を抽出する手順に由来する。原理的には、対応する抽出デザインを二段抽出以外の抽出スキームで実現することも可能である。抽出デザインこそが統計的性質の本質であり、抽出スキームはそのひとつの実現方法にすぎないという両者の関係からすると、抽出スキームにちなんで標本抽出法を命名する慣行は一見奇妙である。
こうした慣行の原因は、抽出スキームが複雑になると、対応する抽出デザインを実現する他の抽出スキームを見つけるのが事実上困難なためなのだろう。抽出デザインと抽出スキームとが一対一に対応しているのであれば、後者にちなんで前者を命名しても差し支えない。実際、ある二段抽出法と同じ抽出デザインを二段抽出以外の方法で実現しようとしても、実行可能な方法は容易に思い浮かばない。
とはいえ、理論的な整理の上では、抽出デザインと抽出スキームとを区別しておくのがよい。推定量の統計的な性質にとっては、抽出デザインが本質的であり、抽出スキームはそのひとつの実現方法であるという関係に変わりはないのだから。
（2011年6月4日）
（作成：西郷 浩；掲示開始：2004年4月30日；最終更新：2011年6月4日）